Introductie

De formules in Calculus A hebben tot nu toe formules met maar een variabele gehad. In Calculus B gaan we echter ook formules met meer dan een variabelen behandelen. Deze formules nemen dan ook meer dan twee dimensies in beslag.

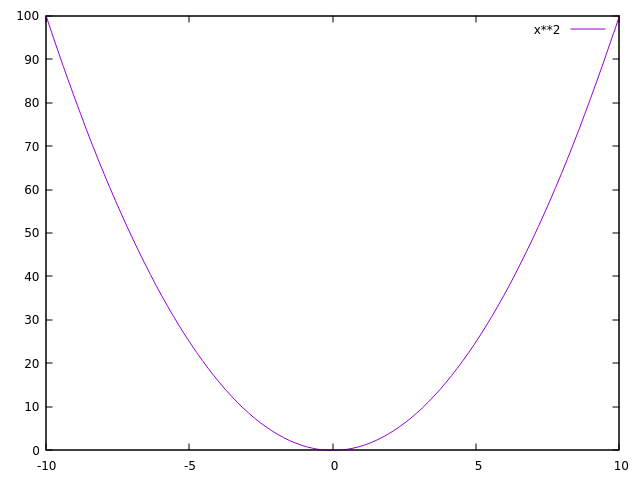
Een voorbeeld van een dergelijke functie is bijvoorbeeld f(x) = x²

Voorbeeld

Een voorbeeld van een functie met twee variabelen is het volume van een massieve ronde cylinder:

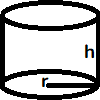
V = r²πh D = {(r, h) ∈ ℝ² : r ≥ 0, h ≥ 0}

Dit is een functie met twee variabelen: r en h;

Voorbeeld

Een ander voorbeeld is de temperatuur in een ruimte. De temperatuur op een bepaalde plek kan beschreven worden door een functie met drie variabelen: de x, y en z coördinaten van de plek in de ruimte. De functie ziet er dan zo uit: T = T(x, y, z) De functie kan ook de temperatuur bepalen aan de hand van de positie en de tijd. In dit geval heeft de functie vier variabelen: x,y en z voor de positie en t voor de tijd. De functie ziet er dan zo uit: T = T(x, y, z, t)

Grafieken van functies met twee variabelen

Grafieken van functies met twee variabelen worden getekend in een driedimensionaal assenstelsel. De notatie is als volgt:

grafiek: f = f(x, y)

vlak: {(x, y, f(x, y)) : (x, y) ∈ D(f)} ⊆ ℝ³

Voorbeeld

Neem bijvoorbeeld f(x, y) = C, D = ℝ² (of de vergelijking z = C). Als je deze tekent in een driedimensionaal assenstelsel krijg je het volgende vlak:

Voorbeeld

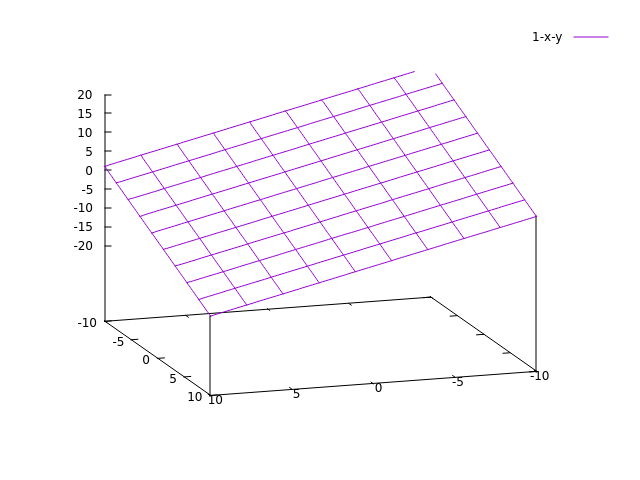
Neem bijvoorbeeld f(x, y) = 1 − x − y, D = ℝ². Dit geeft een schuin vlak dat als volgt getekend wordt:

Niveaukrommen

Niveaukrommen zijn lijnen in een tweedimensionaal assenstelsel die vlakken op de volgende manier beschrijven:

f(x, y) = C

Deze formule geeft krommen in het xy-vlak.
Dit geeft ons het volgende idee:

z = f(x, y) z = C

Dit stelsel geeft een doorsnede met een horizontaal vlak op hoogte c.

Voorbeeld

Neem bijvoorbeeld de formule f(x, y) = 1 − x − y. Als je hier niveaukrommen van neemt krijg je de formule 1 − x − y = C. Deze lijnen kunnen getekend worden in een xy-assenstelsel om een idee van de vorm van een vlak te krijgen.

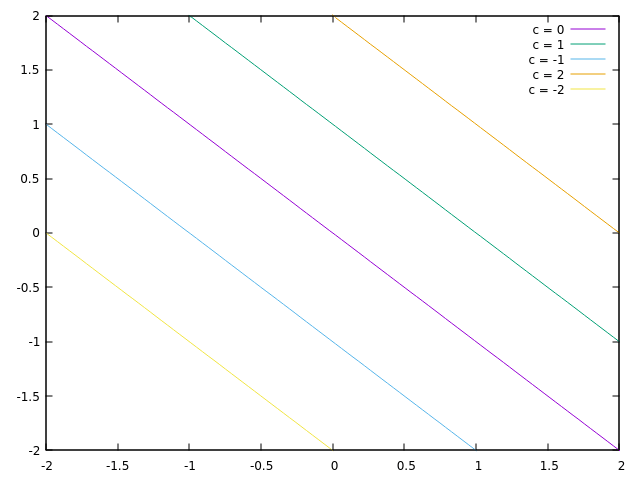
Aangezien de lijnen parallel op gelijke afstand lopen worden hier de niveaukrommen van een plat vlak beschreven. Dit klopt ook als we naar de eerste formule kijken.

Voorbeeld

Neem bijvoorbeeld f(x, y) = √1 - x²-y², D={ (x, y) : x² + y² ≤ 1}.
Als we de niveaukrommen bekijken krijgen we: √1 - x²-y² = C, 0 ≤ C, C² ≤ 1 x² + y² = 1 − C²

Dit geeft de volgende niveaukrommen voor C ∈ {0, 0.1, ..., 1}

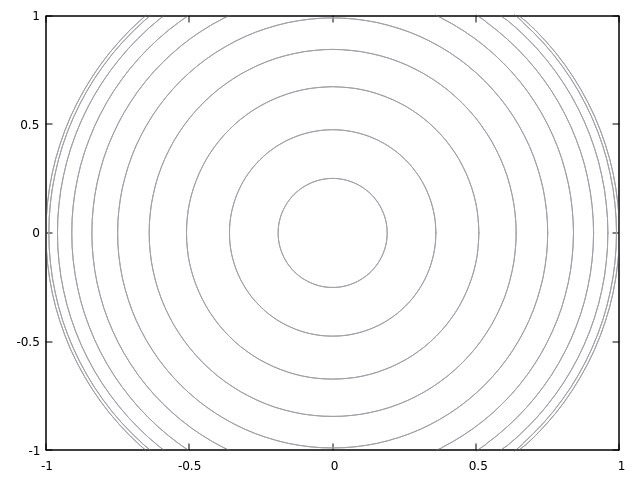
De doorsneden parallel aan het xy-vlak zijn cirkels. We kunnen het ook snijden met x = 0 en y = 0 voor meer informatie. Dit geeft ons het volgende vlak:

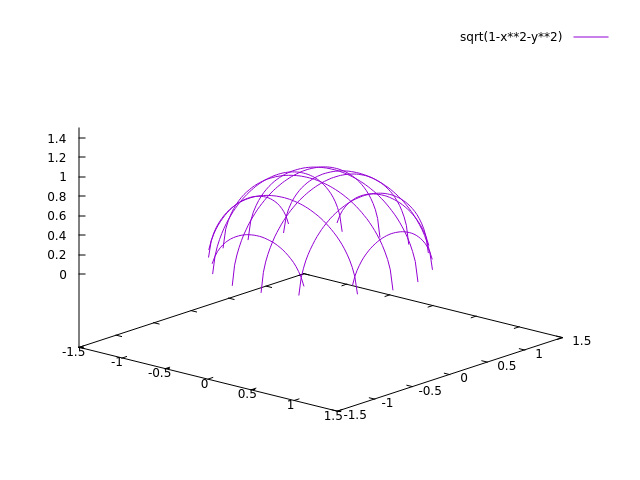
Kwadratische oppervlakten

Kwadratische oppervlakten zijn nulverzamelingen van polynomen van graad twee in drie variabelen. formules voor kwadratische oppervlakten zijn bijvoorbeeld:

Bol

x² + y² + z² = r², met het middenpunt in (0, 0, 0) en radius r.

(x − x₀)² + (y − y₀)² + (z − z₀)² = r² heeft middenpunt in (x₀, y₀, z₀)

Ellipsoïde

x²/a² + y²/b² + z²/c² = 1

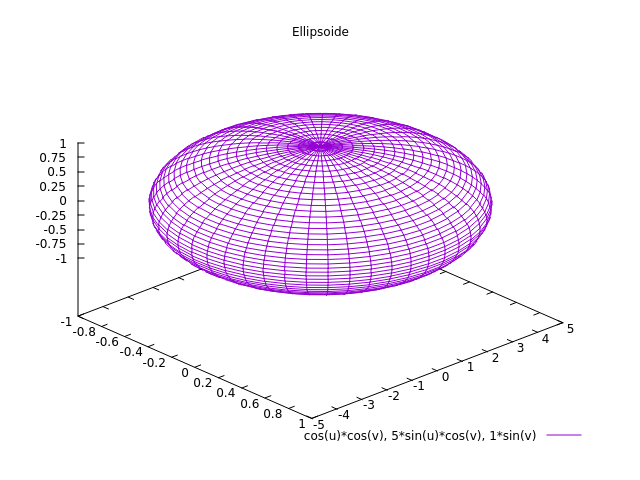
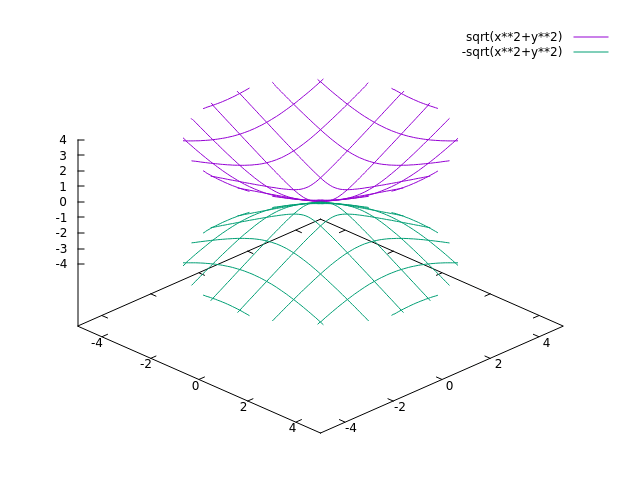
Kegel

z² = x² + y²

Terminologie:

• Bovenste helft = "upper nappe"
  

• Onderste helft = "lower nappe"
  

• middelpunt = "vertex"
  

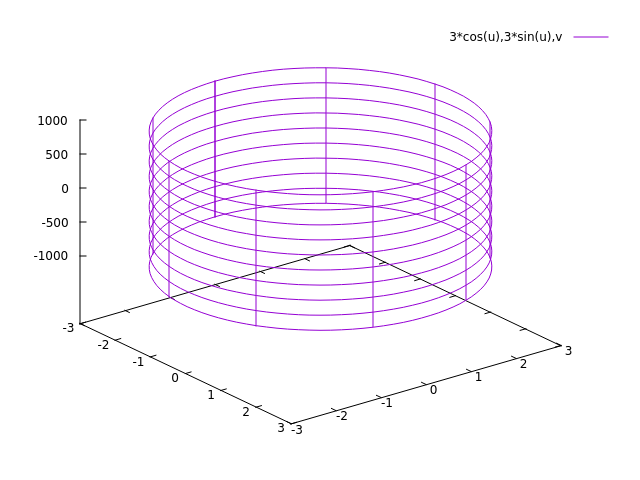
Cilinder

x² + y² = a², z ∈ ℝ geeft een ronde cilinder.

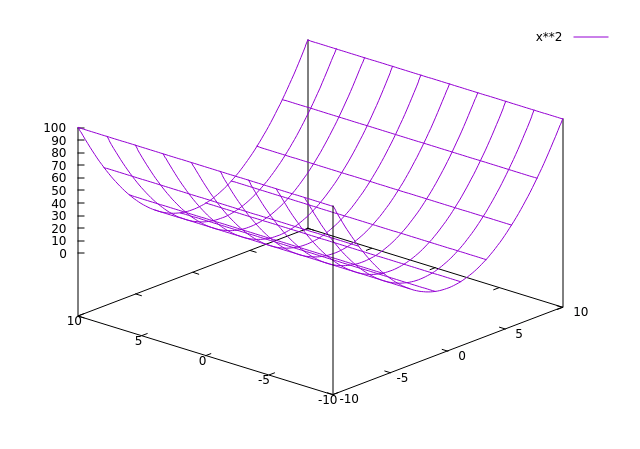
z = x² geeft een parabolische cilinder.

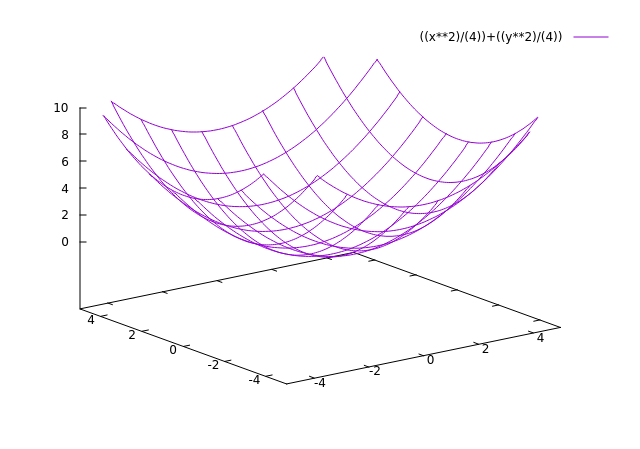
Paraboloïde

z = x²/a² + y²/b² geeft een elliptische paraboloïde.

Een hyperbolische paraboloïde heeft de functie z = x²/a² − y²/b² en heeft de vorm van een zadel.

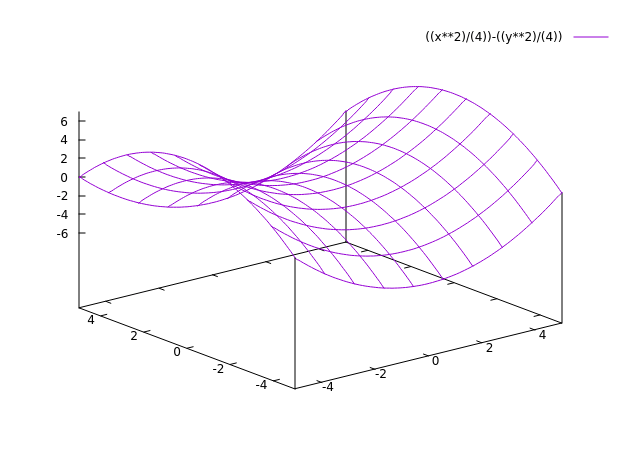
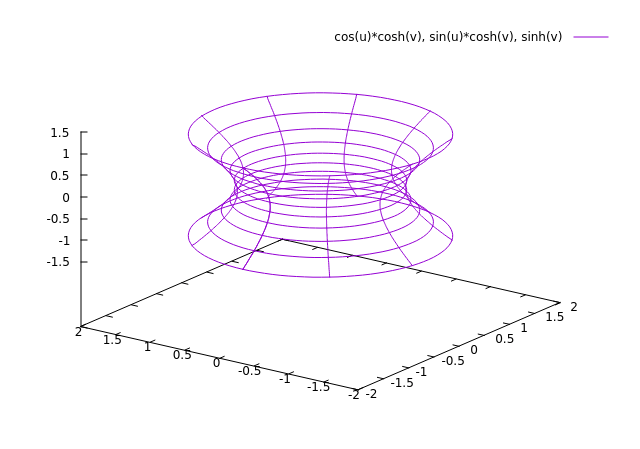
Hyperboloïde

x²/a² + y²/b² − z²/c² = 1. Dit geeft een eenbladige hyperboloïde.

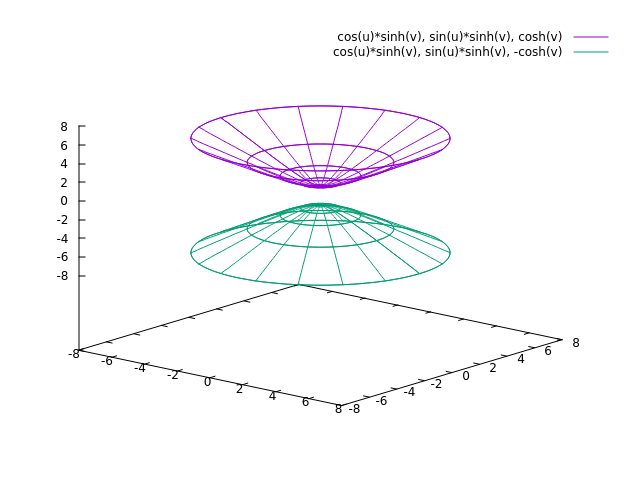
x²/a² + y²/b² − z²/c² = −1 geeft een tweebladige hyperboloïde.

Doorsneden van vlakken

Krommen worden vaak vertegenwoordigd als doorsneden van vlakken.

Voorbeeld

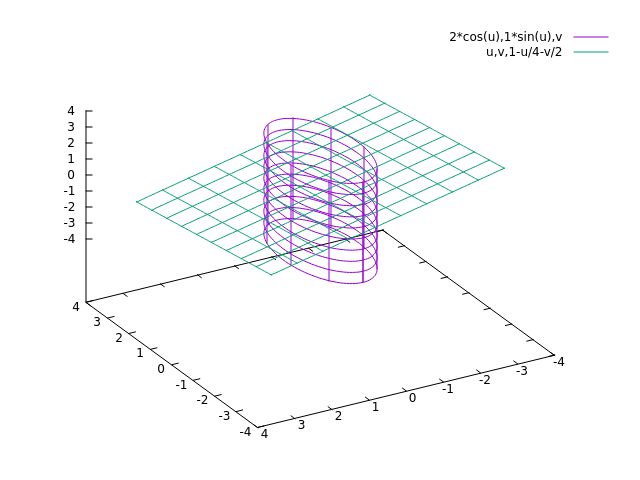
Neem bijvoorbeeld de volgende vlakken:

x + 2y + 4z = 4 vlak x² + 4y² = 4 elliptische cilinder

Als je deze vergelijkingen parametriseert krijg je:

x(t) = 2cos (t) y(t) = sin (t) z(t) = 1/4(4 − 2cos (t) − 2sin (t)

De doorsnede van deze twee vlakken is een ellips met deze formule.